El nivel 3 nos consiguió engañar. Y eso que lo esperábamos… una prueba sobre Asahi Linux va a caer sí o sí; marcan ha estado metiendo miles de horas en este proyecto…
Descomprimiendo el fichero zip que nos adjuntan en la prueba analizamos lo que tenemos:
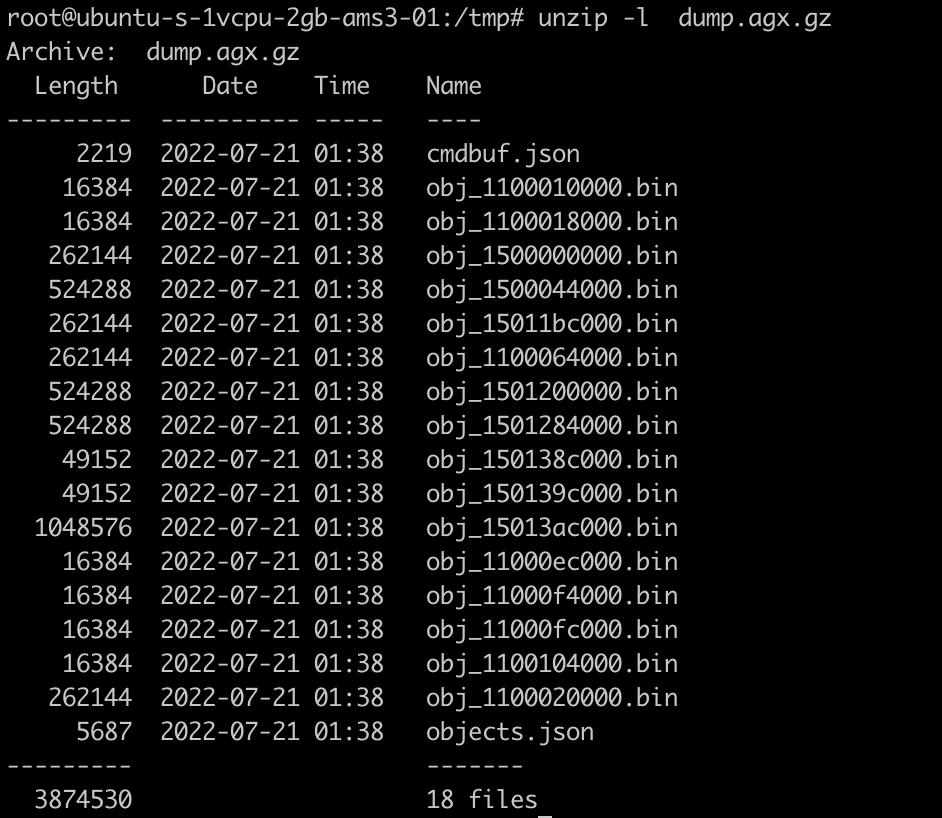
Lo primero, el nombre del gz indica AGX, la arquitectura GPU del M1 (Apple Silicon). Tras leer los posts de Rosenzweig y curiosear el repositorio GitHub de Asahi, llegamos hasta este script que trata de mostrar en pantalla el conejo típico de testing:
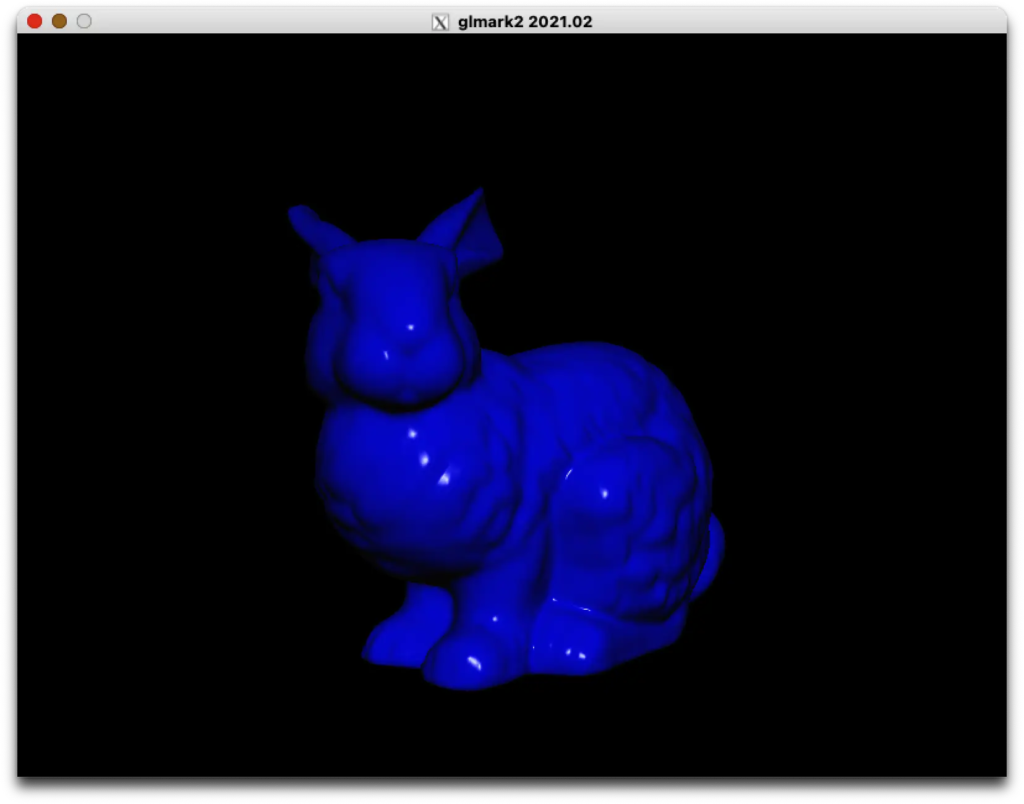
Además, usa variables del cmdbuf.json que nos dan (depth_bias_array, scissor_array…) Así que nuestra idea era ejecutar el código de renderizado del conejo en un m1 y si funcionaba, cambiar los .bin por los que nos daban (y cargar adecuadamente las variables del cmdbuf.json). Había algunos flecos más que arreglar, pero bueno… lo primero era encontra un m1 🙂 Afortunadamente para nuestros bolsillos podemos alquilar el uso de un mac mini m1 por 2.5€ al día.
Seguimos el script de instalación de Asahi hasta el final:
Pero llegamos a un punto interesante… En el último paso Asahi nos pedia apagar el M1 y en el arranque seleccionar Asahi… No contamos con un «pequeño» detalle: en un ordenador remoto al arrancar no tenemos acceso a la pantalla de boot. Así que se nos quedó el m1 en modo rebooting durante toda la party. Dimos la orden de reinstalar el sistema pero no se podía porque estaba en modo rebooting ¯\_(ツ)_/¯
Así que estuvimos dando vueltas y vueltas… sin darnos cuenta de un detalle. Si hay que renderizar algo en pantalla a partir de vértices de un gráfico, necesitaremos esa malla de vértices en 3d… que estará en alguno de los .bin que nos pasan.
En este obj_150138c000.bin, por ejemplo. Si pintamos esos puntos con matplotlib (saludos a @ochoto, que se curró el script):
#!/usr/bin/env python
# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
with open("obj_150138c000.bin", 'rb') as f:
data = np.fromfile(f,dtype="f")
numvertex = len(data) // 3
rshp = data.reshape(numvertex,3)
xs = rshp[:,0]
ys = rshp[:,1]
zs = rshp[:,2]
plt.plot(xs,ys)
plt.show()
Y obtenemos el resultado buscado 🙂
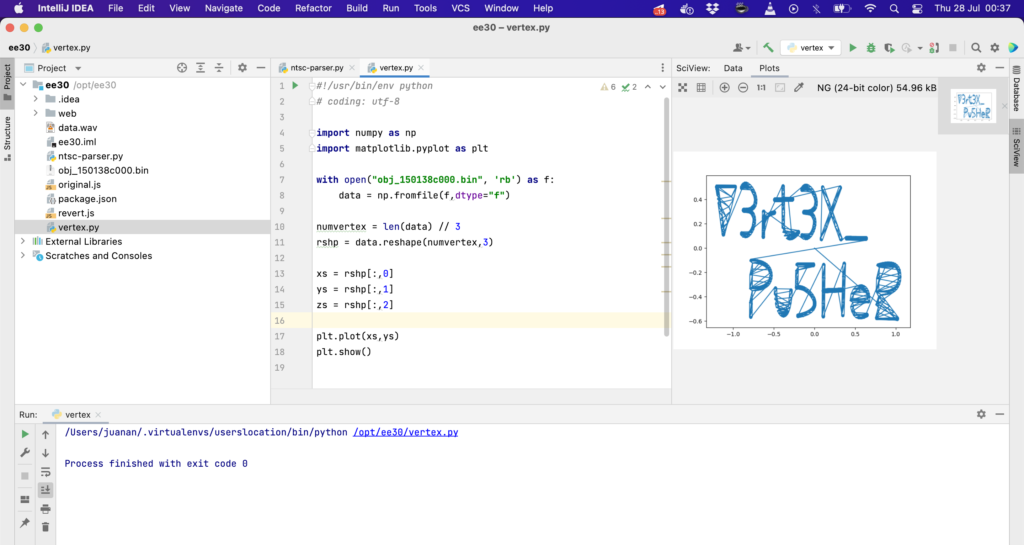
Aupa Juanan, le di una vuelta al script filtrando los puntos 0,0,0 (que hay un montón al final), dando nombre a las columnas (x,y,z) y con un comentario de como comprobar que las coordenadas Z están todas en el mismo plano y por tanto podemos dibujarlo en 2D.
https://gist.github.com/ochoto/7f3b6f4baac08bfa57b0f0094e4a853a